The Genius Blog

Hypothesis Testing Solved Examples(Questions and Solutions)
Here is a list hypothesis testing exercises and solutions. Try to solve a question by yourself first before you look at the solution.
Question 1 In the population, the average IQ is 100 with a standard deviation of 15. A team of scientists want to test a new medication to see if it has either a positive or negative effect on intelligence, or not effect at all. A sample of 30 participants who have taken the medication has a mean of 140. Did the medication affect intelligence? View Solution to Question 1
A professor wants to know if her introductory statistics class has a good grasp of basic math. Six students are chosen at random from the class and given a math proficiency test. The professor wants the class to be able to score above 70 on the test. The six students get the following scores:62, 92, 75, 68, 83, 95. Can the professor have 90% confidence that the mean score for the class on the test would be above 70. Solution to Question 2
Question 3 In a packaging plant, a machine packs cartons with jars. It is supposed that a new machine would pack faster on the average than the machine currently used. To test the hypothesis, the time it takes each machine to pack ten cartons are recorded. The result in seconds is as follows.
| 42.1 | 42.7 |
| 41 | 43.6 |
| 41.3 | 43.8 |
| 41.8 | 43.3 |
| 42.4 | 42.5 |
| 42.8 | 43.5 |
| 43.2 | 43.1 |
| 42.3 | 41.7 |
| 41.8 | 44 |
| 42.7 | 44.1 |
Do the data provide sufficient evidence to conclude that, on the average, the new machine packs faster? Perform the required hypothesis test at the 5% level of significance. Solution to Question 3
Question 4 We want to compare the heights in inches of two groups of individuals. Here are the measurements: X: 175, 168, 168, 190, 156, 181, 182, 175, 174, 179 Y: 120, 180, 125, 188, 130, 190, 110, 185, 112, 188 Solution to Question 4
Question 5 A clinic provides a program to help their clients lose weight and asks a consumer agency to investigate the effectiveness of the program. The agency takes a sample of 15 people, weighing each person in the sample before the program begins and 3 months later. The results a tabulated below
Determine is the program is effective. Solution to Question 5
Question 6 A sample of 20 students were selected and given a diagnostic module prior to studying for a test. And then they were given the test again after completing the module. . The result of the students scores in the test before and after the test is tabulated below.
We want to see if there is significant improvement in the student’s performance due to this teaching method Solution to Question 6
Question 7 A study was performed to test wether cars get better mileage on premium gas than on regular gas. Each of 10 cars was first filled with regular or premium gas, decided by a coin toss, and the mileage for the tank was recorded. The mileage was recorded again for the same cars using other kind of gasoline. Determine wether cars get significantly better mileage with premium gas.
Mileage with regular gas: 16,20,21,22,23,22,27,25,27,28 Mileage with premium gas: 19, 22,24,24,25,25,26,26,28,32 Solution to Question 7
Question 8 An automatic cutter machine must cut steel strips of 1200 mm length. From a preliminary data, we checked that the lengths of the pieces produced by the machine can be considered as normal random variables with a 3mm standard deviation. We want to make sure that the machine is set correctly. Therefore 16 pieces of the products are randomly selected and weight. The figures were in mm: 1193,1196,1198,1195,1198,1199,1204,1193,1203,1201,1196,1200,1191,1196,1198,1191 Examine wether there is any significant deviation from the required size Solution to Question 8
Question 9 Blood pressure reading of ten patients before and after medication for reducing the blood pressure are as follows
Patient: 1,2,3,4,5,6,7,8,9,10 Before treatment: 86,84,78,90,92,77,89,90,90,86 After treatment: 80,80,92,79,92,82,88,89,92,83
Test the null hypothesis of no effect agains the alternate hypothesis that medication is effective. Execute it with Wilcoxon test Solution to Question 9
Question on ANOVA Sussan Sound predicts that students will learn most effectively with a constant background sound, as opposed to an unpredictable sound or no sound at all. She randomly divides 24 students into three groups of 8 each. All students study a passage of text for 30 minutes. Those in group 1 study with background sound at a constant volume in the background. Those in group 2 study with nose that changes volume periodically. Those in group 3 study with no sound at all. After studying, all students take a 10 point multiple choice test over the material. Their scores are tabulated below.
Group1: Constant sound: 7,4,6,8,6,6,2,9 Group 2: Random sound: 5,5,3,4,4,7,2,2 Group 3: No sound at all: 2,4,7,1,2,1,5,5 Solution to Question 10
Question 11 Using the following three groups of data, perform a one-way analysis of variance using α = 0.05.
| 51 | 23 | 56 |
| 45 | 43 | 76 |
| 33 | 23 | 74 |
| 45 | 43 | 87 |
| 67 | 45 | 56 |
Solution to Question 11
Question 12 In a packaging plant, a machine packs cartons with jars. It is supposed that a new machine would pack faster on the average than the machine currently used. To test the hypothesis, the time it takes each machine to pack ten cartons are recorded. The result in seconds is as follows.
New Machine: 42,41,41.3,41.8,42.4,42.8,43.2,42.3,41.8,42.7 Old Machine: 42.7,43.6,43.8,43.3,42.5,43.5,43.1,41.7,44,44.1
Perform an F-test to determine if the null hypothesis should be accepted. Solution to Question 12
Question 13 A random sample 500 U.S adults are questioned about their political affiliation and opinion on a tax reform bill. We need to test if the political affiliation and their opinon on a tax reform bill are dependent, at 5% level of significance. The observed contingency table is given below.
| total | ||||
| 138 | 83 | 64 | 285 | |
| 64 | 67 | 84 | 215 | |
| total | 202 | 150 | 148 | 500 |
Solution to Question 13
Question 14 Can a dice be considered regular which is showing the following frequency distribution during 1000 throws?
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 182 | 154 | 162 | 175 | 151 | 176 |
Solution to Question 14
Solution to Question 15
Question 16 A newly developed muesli contains five types of seeds (A, B, C, D and E). The percentage of which is 35%, 25%, 20%, 10% and 10% according to the product information. In a randomly selected muesli, the following volume distribution was found.
| Component | A | B | C | D | E |
| Number of Pieces | 184 | 145 | 100 | 63 | 63 |
Lets us decide about the null hypothesis whether the composition of the sample corresponds to the distribution indicated on the packaging at alpha = 0.1 significance level. Solution to Question 16
Question 17 A research team investigated whether there was any significant correlation between the severity of a certain disease runoff and the age of the patients. During the study, data for n = 200 patients were collected and grouped according to the severity of the disease and the age of the patient. The table below shows the result
| 41 | 34 | 9 | ||
| 25 | 25 | 12 | ||
| 6 | 33 | 15 | ||
Let us decided about the correlation between the age of the patients and the severity of disease progression. Solution to Question 17
Question 18 A publisher is interested in determine which of three book cover is most attractive. He interviews 400 people in each of the three states (California, Illinois and New York), and asks each person which of the cover he or she prefers. The number of preference for each cover is as follows:
| 81 | 60 | 182 | 323 | |
| 78 | 93 | 95 | 266 | |
| 241 | 247 | 123 | 611 | |
| 400 | 400 | 400 | 1200 |
Do these data indicate that there are regional differences in people’s preferences concerning these covers? Use the 0.05 level of significance. Solution to Question 18
Question 19 Trees planted along the road were checked for which ones are healthy(H) or diseased (D) and the following arrangement of the trees were obtained:
H H H H D D D H H H H H H H D D H H D D D
Test at the = 0.05 significance wether this arrangement may be regarded as random
Solution to Question 19
Question 20 Suppose we flip a coin n = 15 times and come up with the following arrangements
H T T T H H T T T T H H T H H
(H = head, T = tail)
Test at the alpha = 0.05 significance level whether this arrangement may be regarded as random.
Solution to Question 20
kindsonthegenius
You might also like, hypothesis testing problem – question 1(in a population, the average iq…, chi-square goodness of fit test – question 16 ( a newly developed muesli…), question 13 – chi-square test for independence step by step procedure(political affiliation…).
I am really impressed with your writing abilities as well as with the structure to your weblog. Is this a paid subject matter or did you modify it yourself?
Either way stay up the excellent high quality writing, it’s uncommon to look a great blog like this one these days..
Below are given the gain in weights (in lbs.) of pigs fed on two diet A and B Dieta 25 32 30 34 24 14 32 24 30 31 35 25 – – DietB 44 34 22 10 47 31 40 30 32 35 18 21 35 29
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Hypothesis Testing | A Step-by-Step Guide with Easy Examples
Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
There are 5 main steps in hypothesis testing:
- State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
- Collect data in a way designed to test the hypothesis.
- Perform an appropriate statistical test .
- Decide whether to reject or fail to reject your null hypothesis.
- Present the findings in your results and discussion section.
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
Table of contents
Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.
After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.
The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
- H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.
Prevent plagiarism. Run a free check.
For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.
There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).
If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.
Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.
Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
- an estimate of the difference in average height between the two groups.
- a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.
In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.
In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .
In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.
In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.
However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.
If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”
These are superficial differences; you can see that they mean the same thing.
You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.
If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved July 2, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
S.3.3 hypothesis testing examples.
- Example: Right-Tailed Test
- Example: Left-Tailed Test
- Example: Two-Tailed Test
Brinell Hardness Scores
An engineer measured the Brinell hardness of 25 pieces of ductile iron that were subcritically annealed. The resulting data were:
| Brinell Hardness of 25 Pieces of Ductile Iron | ||||||||
|---|---|---|---|---|---|---|---|---|
| 170 | 167 | 174 | 179 | 179 | 187 | 179 | 183 | 179 |
| 156 | 163 | 156 | 187 | 156 | 167 | 156 | 174 | 170 |
| 183 | 179 | 174 | 179 | 170 | 159 | 187 | ||
The engineer hypothesized that the mean Brinell hardness of all such ductile iron pieces is greater than 170. Therefore, he was interested in testing the hypotheses:
H 0 : μ = 170 H A : μ > 170
The engineer entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:
Descriptive Statistics
| N | Mean | StDev | SE Mean | 95% Lower Bound |
|---|---|---|---|---|
| 25 | 172.52 | 10.31 | 2.06 | 168.99 |
$\mu$: mean of Brinelli
Null hypothesis H₀: $\mu$ = 170 Alternative hypothesis H₁: $\mu$ > 170
| T-Value | P-Value |
|---|---|
| 1.22 | 0.117 |
The output tells us that the average Brinell hardness of the n = 25 pieces of ductile iron was 172.52 with a standard deviation of 10.31. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 10.31 by the square root of n = 25, is 2.06). The test statistic t * is 1.22, and the P -value is 0.117.
If the engineer set his significance level α at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were greater than 1.7109 (determined using statistical software or a t -table):
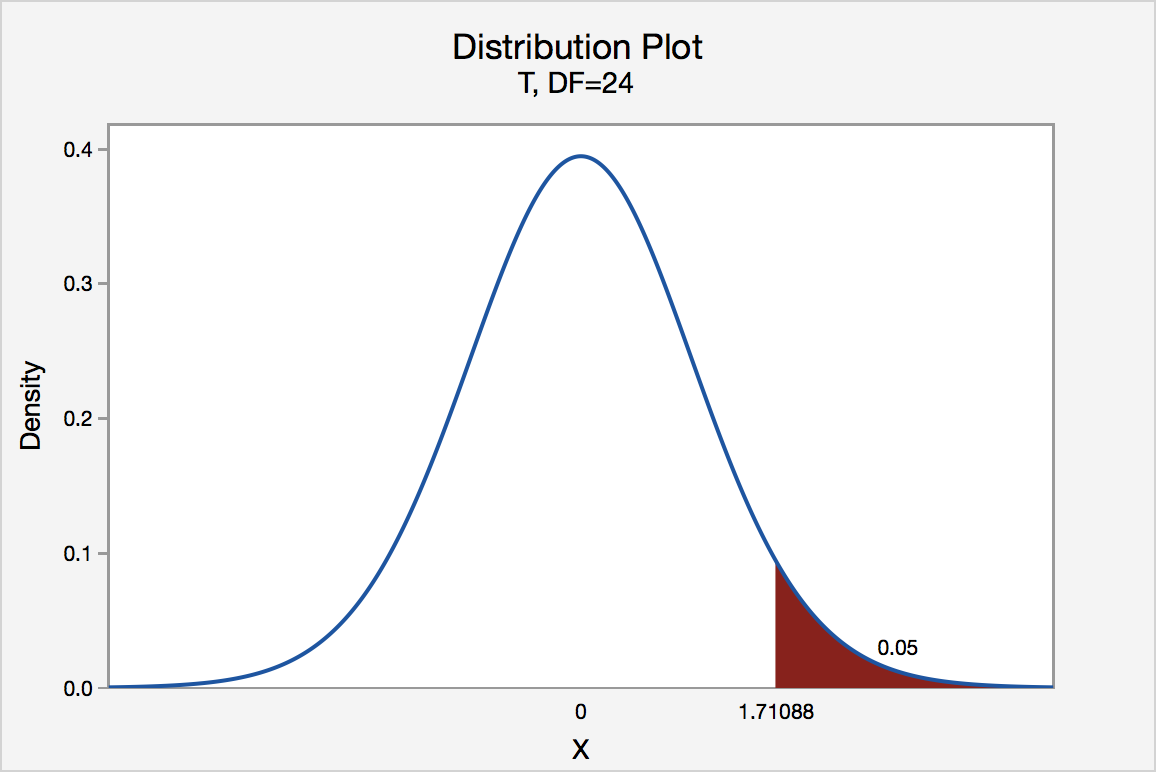
Since the engineer's test statistic, t * = 1.22, is not greater than 1.7109, the engineer fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.
If the engineer used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 24 curve and to the right of the test statistic t * = 1.22:
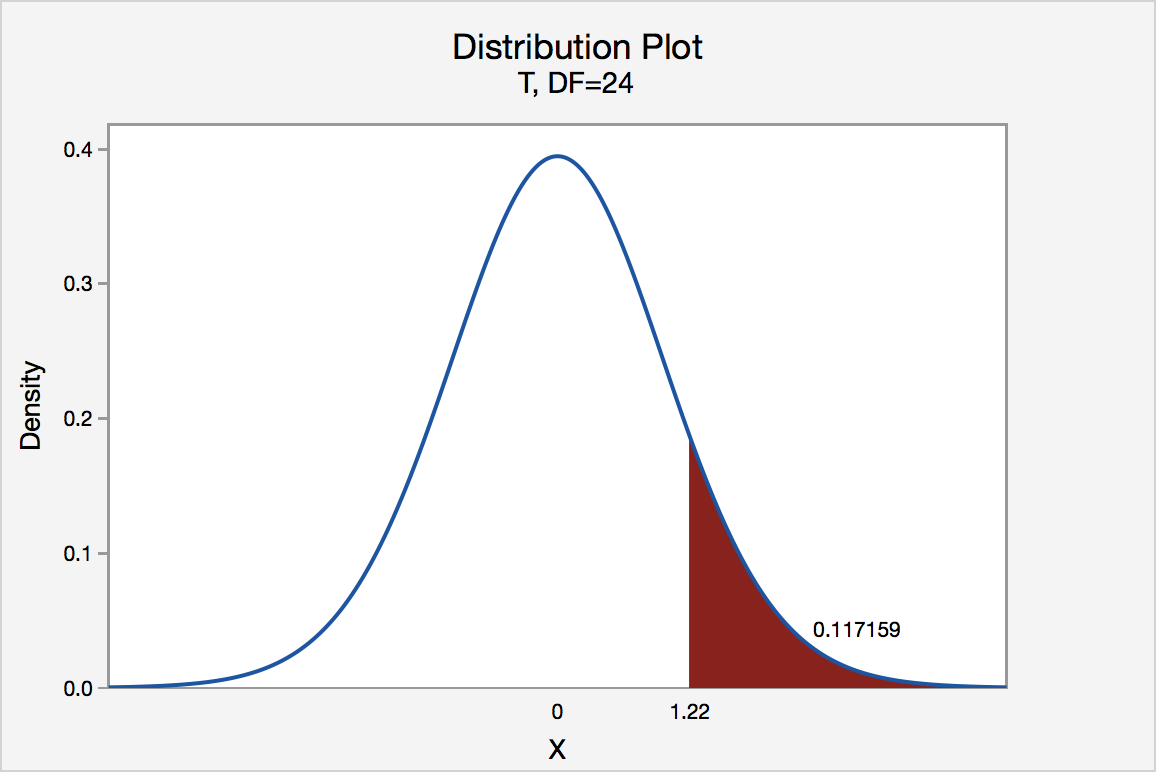
In the output above, Minitab reports that the P -value is 0.117. Since the P -value, 0.117, is greater than \(\alpha\) = 0.05, the engineer fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.
Note that the engineer obtains the same scientific conclusion regardless of the approach used. This will always be the case.
Height of Sunflowers
A biologist was interested in determining whether sunflower seedlings treated with an extract from Vinca minor roots resulted in a lower average height of sunflower seedlings than the standard height of 15.7 cm. The biologist treated a random sample of n = 33 seedlings with the extract and subsequently obtained the following heights:
| Heights of 33 Sunflower Seedlings | ||||||||
|---|---|---|---|---|---|---|---|---|
| 11.5 | 11.8 | 15.7 | 16.1 | 14.1 | 10.5 | 9.3 | 15.0 | 11.1 |
| 15.2 | 19.0 | 12.8 | 12.4 | 19.2 | 13.5 | 12.2 | 13.3 | |
| 16.5 | 13.5 | 14.4 | 16.7 | 10.9 | 13.0 | 10.3 | 15.8 | |
| 15.1 | 17.1 | 13.3 | 12.4 | 8.5 | 14.3 | 12.9 | 13.5 | |
The biologist's hypotheses are:
H 0 : μ = 15.7 H A : μ < 15.7
The biologist entered her data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. She obtained the following output:
| N | Mean | StDev | SE Mean | 95% Upper Bound |
|---|---|---|---|---|
| 33 | 13.664 | 2.544 | 0.443 | 14.414 |
$\mu$: mean of Height
Null hypothesis H₀: $\mu$ = 15.7 Alternative hypothesis H₁: $\mu$ < 15.7
| T-Value | P-Value |
|---|---|
| -4.60 | 0.000 |
The output tells us that the average height of the n = 33 sunflower seedlings was 13.664 with a standard deviation of 2.544. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 13.664 by the square root of n = 33, is 0.443). The test statistic t * is -4.60, and the P -value, 0.000, is to three decimal places.
Minitab Note. Minitab will always report P -values to only 3 decimal places. If Minitab reports the P -value as 0.000, it really means that the P -value is 0.000....something. Throughout this course (and your future research!), when you see that Minitab reports the P -value as 0.000, you should report the P -value as being "< 0.001."
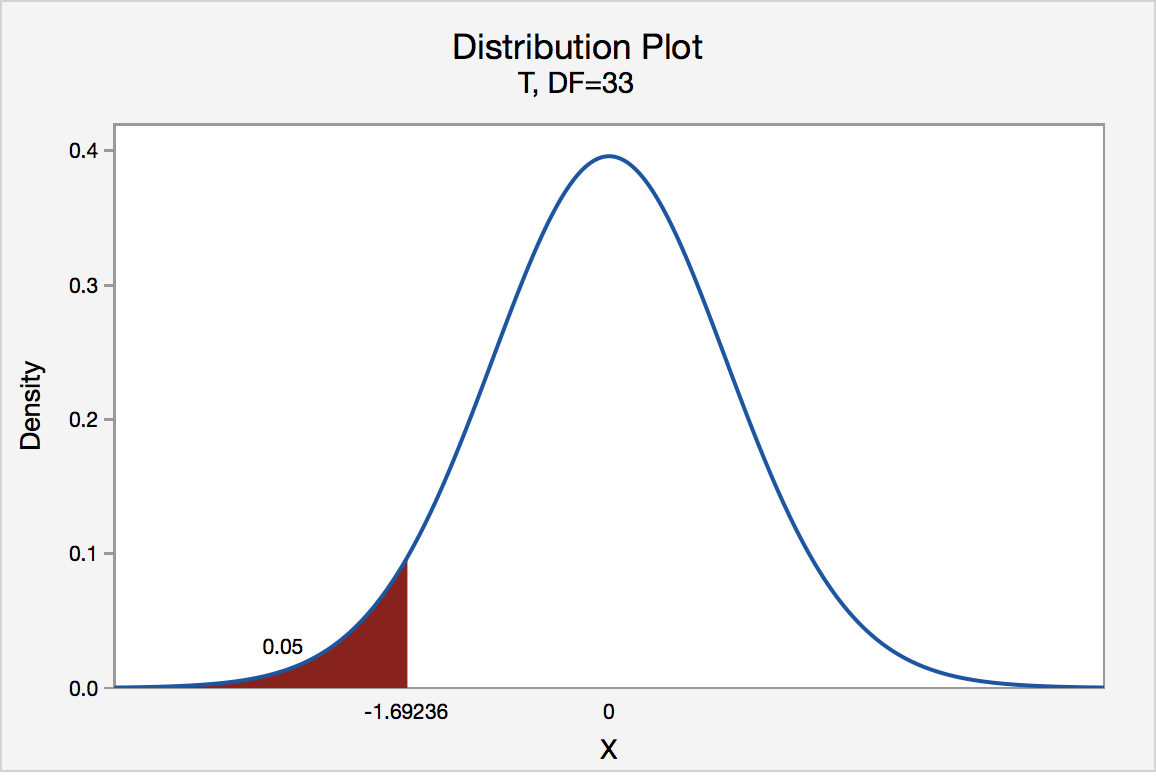
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t * were less than -1.6939 (determined using statistical software or a t -table):s-3-3
Since the biologist's test statistic, t * = -4.60, is less than -1.6939, the biologist rejects the null hypothesis. That is, the test statistic falls in the "critical region." There is sufficient evidence, at the α = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.
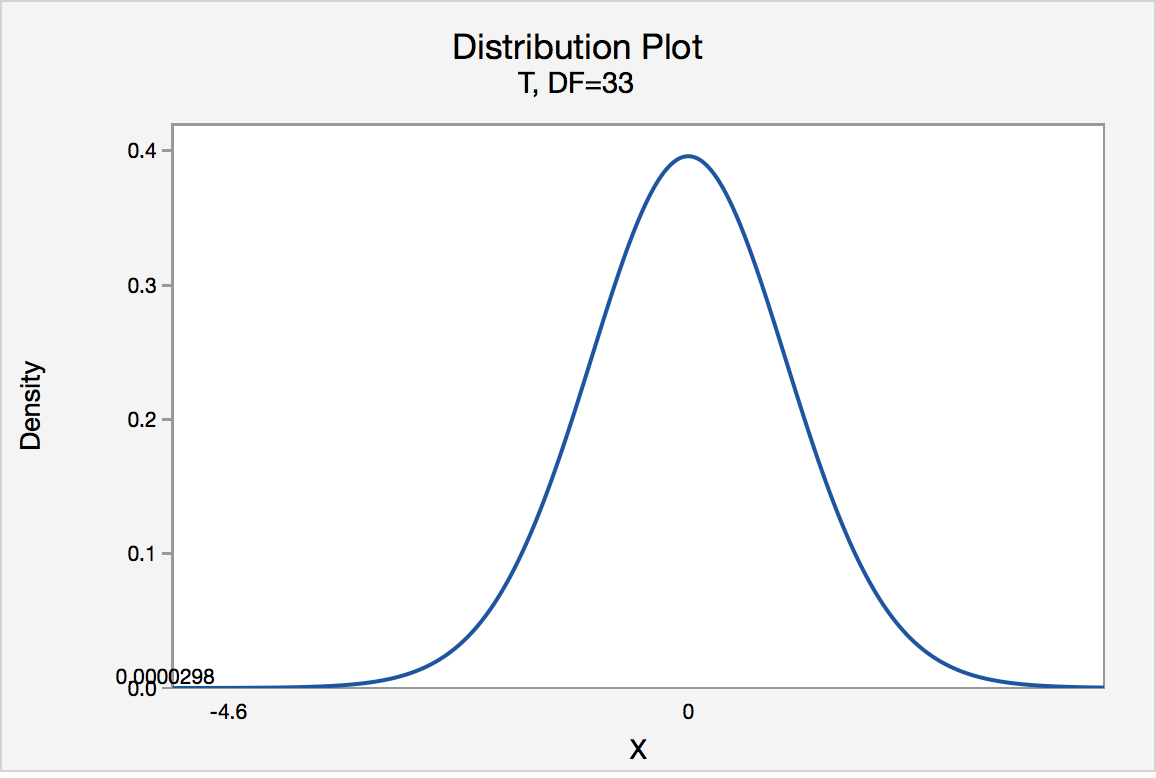
If the biologist used the P -value approach to conduct her hypothesis test, she would determine the area under a t n - 1 = t 32 curve and to the left of the test statistic t * = -4.60:
In the output above, Minitab reports that the P -value is 0.000, which we take to mean < 0.001. Since the P -value is less than 0.001, it is clearly less than \(\alpha\) = 0.05, and the biologist rejects the null hypothesis. There is sufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.
Note again that the biologist obtains the same scientific conclusion regardless of the approach used. This will always be the case.
Gum Thickness
A manufacturer claims that the thickness of the spearmint gum it produces is 7.5 one-hundredths of an inch. A quality control specialist regularly checks this claim. On one production run, he took a random sample of n = 10 pieces of gum and measured their thickness. He obtained:
| Thicknesses of 10 Pieces of Gum | ||||
|---|---|---|---|---|
| 7.65 | 7.60 | 7.65 | 7.70 | 7.55 |
| 7.55 | 7.40 | 7.40 | 7.50 | 7.50 |
The quality control specialist's hypotheses are:
H 0 : μ = 7.5 H A : μ ≠ 7.5
The quality control specialist entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:
| N | Mean | StDev | SE Mean | 95% CI for $\mu$ |
|---|---|---|---|---|
| 10 | 7.550 | 0.1027 | 0.0325 | (7.4765, 7.6235) |
$\mu$: mean of Thickness
Null hypothesis H₀: $\mu$ = 7.5 Alternative hypothesis H₁: $\mu \ne$ 7.5
| T-Value | P-Value |
|---|---|
| 1.54 | 0.158 |
The output tells us that the average thickness of the n = 10 pieces of gums was 7.55 one-hundredths of an inch with a standard deviation of 0.1027. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 0.1027 by the square root of n = 10, is 0.0325). The test statistic t * is 1.54, and the P -value is 0.158.
If the quality control specialist sets his significance level \(\alpha\) at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were less than -2.2616 or greater than 2.2616 (determined using statistical software or a t -table):
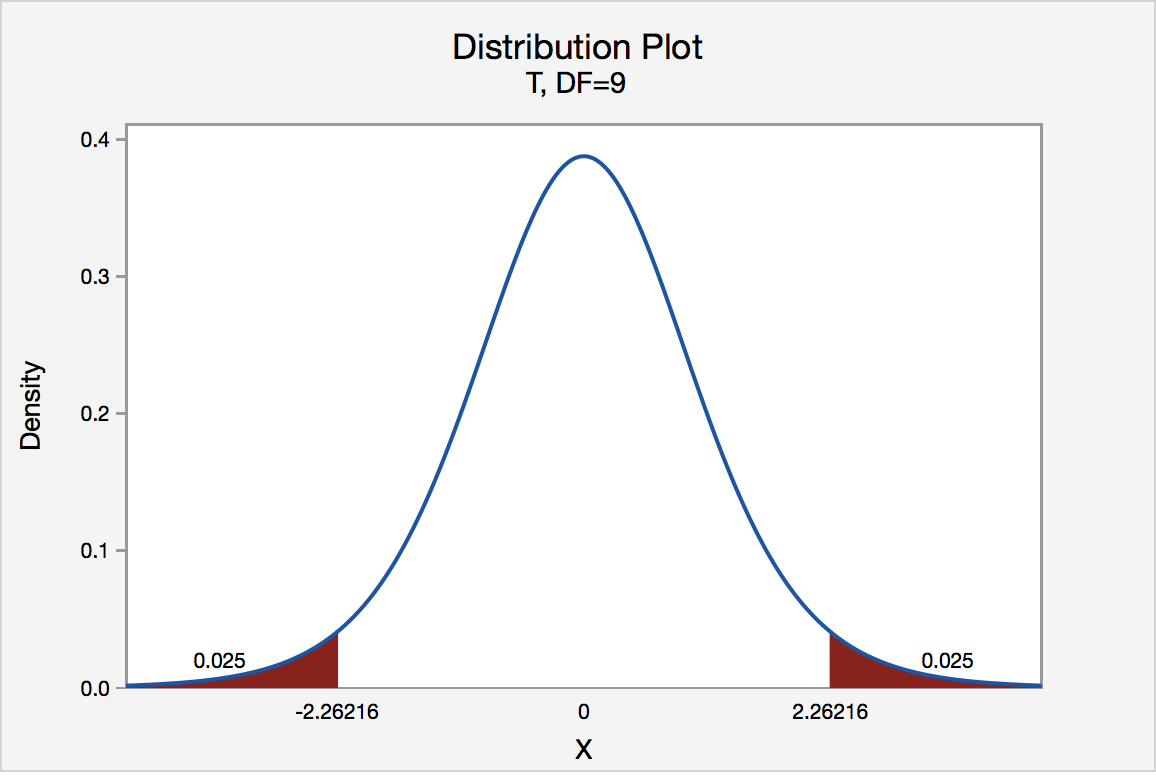
Since the quality control specialist's test statistic, t * = 1.54, is not less than -2.2616 nor greater than 2.2616, the quality control specialist fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all of the manufacturer's spearmint gum differs from 7.5 one-hundredths of an inch.
If the quality control specialist used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 9 curve, to the right of 1.54 and to the left of -1.54:
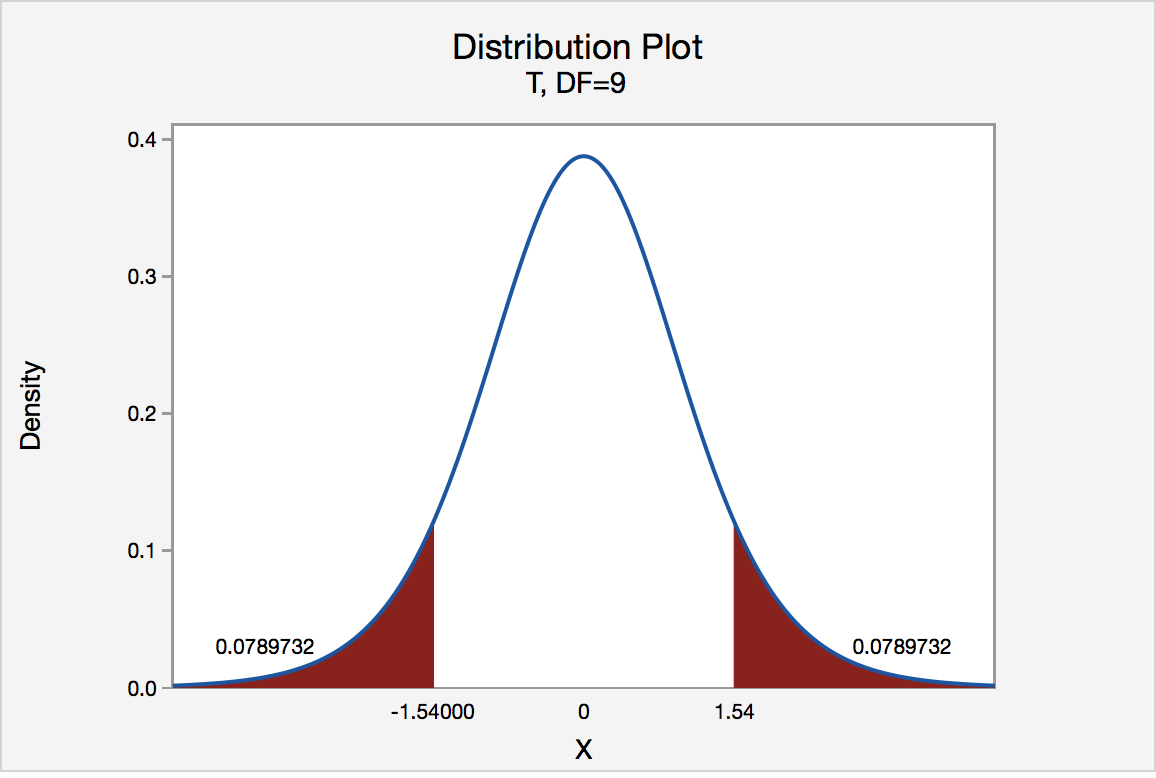
In the output above, Minitab reports that the P -value is 0.158. Since the P -value, 0.158, is greater than \(\alpha\) = 0.05, the quality control specialist fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all pieces of spearmint gum differs from 7.5 one-hundredths of an inch.
Note that the quality control specialist obtains the same scientific conclusion regardless of the approach used. This will always be the case.
In our review of hypothesis tests, we have focused on just one particular hypothesis test, namely that concerning the population mean \(\mu\). The important thing to recognize is that the topics discussed here — the general idea of hypothesis tests, errors in hypothesis testing, the critical value approach, and the P -value approach — generally extend to all of the hypothesis tests you will encounter.
9.4 Full Hypothesis Test Examples
Tests on means, example 9.8.
Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds . His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey's mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05. Assume that the swim times for the 25-yard freestyle are normal.
Set up the Hypothesis Test:
Since the problem is about a mean, this is a test of a single population mean .
H 0 : μ = 16.43 H a : μ < 16.43
For Jeffrey to swim faster, his time will be less than 16.43 seconds. The "<" tells you this is left-tailed.
Determine the distribution needed:
Random variable: X ¯ X ¯ = the mean time to swim the 25-yard freestyle.
Distribution for the test: X ¯ X ¯ is normal (population standard deviation is known: σ = 0.8)
X ¯ ~ N ( μ , σ X n ) X ¯ ~ N ( μ , σ X n ) Therefore, X ¯ ~ N ( 16.43 , 0.8 15 ) X ¯ ~ N ( 16.43 , 0.8 15 )
μ = 16.43 comes from H 0 and not the data. σ = 0.8, and n = 15.
Calculate the p -value using the normal distribution for a mean:
p -value = P ( x ¯ x ¯ < 16) = 0.0187 where the sample mean in the problem is given as 16.
p -value = 0.0187 (This is called the actual level of significance .) The p -value is the area to the left of the sample mean is given as 16.
μ = 16.43 comes from H 0 . Our assumption is μ = 16.43.
Interpretation of the p -value: If H 0 is true , there is a 0.0187 probability (1.87%)that Jeffrey's mean time to swim the 25-yard freestyle is 16 seconds or less. Because a 1.87% chance is small, the mean time of 16 seconds or less is unlikely to have happened randomly. It is a rare event.
Compare α and the p -value:
α = 0.05 p -value = 0.0187 α > p -value
Make a decision: Since α > α > p -value, reject H 0 .
This indicates that you reject the null hypothesis that the mean time to swim the 25-yard freestyle is at least 16.43 seconds.
Conclusion: At the 5% significance level, there is sufficient evidence that Jeffrey's mean time to swim the 25-yard freestyle is less than 16.43 seconds. Thus, based on the sample data, we conclude that Jeffrey swims faster using the new goggles.
The Type I and Type II errors for this problem are as follows: The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in at least 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.)
The Type II error is that there is not evidence to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually does swim the 25-yard free-style, on average, in less than 16.43 seconds. (Do not reject the null hypothesis when the null hypothesis is false.)
The mean throwing distance of a football for Marco, a high school quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset α = 0.05. Assume the throw distances for footballs are normal.
First, determine what type of test this is, set up the hypothesis test, find the p -value, sketch the graph, and state your conclusion.
Example 9.9
Jasmine has just begun her new job on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of 108 dollars with a standard deviation of 12 dollars. Test at 5% significance that the population mean is at least 100 dollars against the alternative that it is less than 100 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jasmine has met this requirement at the significance level of 95%?
- H 0 : µ ≤ 100 H a : µ > 100 The null and alternative hypothesis are for the parameter µ because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not "too high" a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis.
- Test statistic: t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67 t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67
- Critical value: t a = 1.753 t a = 1.753 with n-1 degrees of freedom= 15
The test statistic is a Student's t because the sample size is below 30; therefore, we cannot use the normal distribution. Comparing the calculated value of the test statistic and the critical value of t t ( t a ) ( t a ) at a 5% significance level, we see that the calculated value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we cannot accept the null hypothesis. There is evidence that supports Jasmine's performance meets company standards.
It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, state your conclusion, and identify the Type I errors.
Example 9.10
A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, s 2 s 2 . Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of significance in the analysis should be 99%.
Again we will follow the steps in our analysis of this problem.
STEP 1 : Set the Null and Alternative Hypothesis. The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:
STEP 2 : Decide the level of significance and draw the graph showing the critical value.
This problem has already set the level of significance at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because this is a continuous random variable and we are interested in the mean, and the sample size is greater than 30, the appropriate distribution is the normal distribution and the relevant critical value is 2.575 from the normal table or the t-table at 0.005 column and infinite degrees of freedom. We draw the graph and mark these points.
STEP 3 : Calculate sample parameters and the test statistic. The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, s, is 0.173. With this information we calculate the test statistic as -3.07, and mark it on the graph.
STEP 4 : Compare test statistic and the critical values Now we compare the test statistic and the critical value by placing the test statistic on the graph. We see that the test statistic is in the tail, decidedly greater than the critical value of 2.575. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard deviations. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3 plus standard deviations away and thus we cannot accept the null hypothesis.
STEP 5 : Reach a Conclusion
Three standard deviations of a test statistic will guarantee that the test will fail. The probability that anything is within three standard deviations is almost zero. Actually it is 0.0026 on the normal distribution, which is certainly almost zero in a practical sense. Our formal conclusion would be “ At a 99% level of significance we cannot accept the hypothesis that the sample mean came from a distribution with a mean of 8 ounces” Or less formally, and getting to the point, “At a 99% level of significance we conclude that the machine is under filling the bottles and is in need of repair”.
Try It 9.10
A company records the mean time of employees working in a day. The mean comes out to be 475 minutes, with a standard deviation of 45 minutes. A manager recorded times of 20 employees. The times of working were (frequencies are in parentheses) 460(3); 465(2); 470(3); 475(1); 480(6); 485(3); 490(2).
Conduct a hypothesis test using a 2.5% level of significance to determine if the mean time is more than 475 .
Hypothesis Test for Proportions
Just as there were confidence intervals for proportions, or more formally, the population parameter p of the binomial distribution, there is the ability to test hypotheses concerning p .
The population parameter for the binomial is p . The estimated value (point estimate) for p is p′ where p′ = x/n , x is the number of successes in the sample and n is the sample size.
When you perform a hypothesis test of a population proportion p , you take a simple random sample from the population. The conditions for a binomial distribution must be met, which are: there are a certain number n of independent trials meaning random sampling, the outcomes of any trial are binary, success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np′ and nq′ must both be greater than five ( np′ > 5 and nq′ > 5). In this case the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = np μ = np and σ = npq σ = npq . Remember that q = 1 – p q = 1 – p . There is no distribution that can correct for this small sample bias and thus if these conditions are not met we simply cannot test the hypothesis with the data available at that time. We met this condition when we first were estimating confidence intervals for p .
Again, we begin with the standardizing formula modified because this is the distribution of a binomial.
Substituting p 0 p 0 , the hypothesized value of p , we have:
This is the test statistic for testing hypothesized values of p , where the null and alternative hypotheses take one of the following forms:
| Two-tailed test | One-tailed test | One-tailed test |
|---|---|---|
| H : p = p | H : p ≤ p | H : p ≥ p |
| H : p ≠ p | H : p > p | H : p < p |
The decision rule stated above applies here also: if the calculated value of Z c shows that the sample proportion is "too many" standard deviations from the hypothesized proportion, the null hypothesis cannot be accepted. The decision as to what is "too many" is pre-determined by the analyst depending on the level of significance required in the test.
Example 9.11
The mortgage department of a large bank is interested in the nature of loans of first-time borrowers. This information will be used to tailor their marketing strategy. They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is the same or different from 50% . They sample 100 first-time borrowers and find 53 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of significance.
STEP 1 : Set the null and alternative hypothesis.
H 0 : p = 0.50 H a : p ≠ 0.50
The words "is the same or different from" tell you this is a two-tailed test. The Type I and Type II errors are as follows: The Type I error is to conclude that the proportion of borrowers is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true). The Type II error is there is not enough evidence to conclude that the proportion of first time borrowers differs from 50% when, in fact, the proportion does differ from 50%. (You fail to reject the null hypothesis when the null hypothesis is false.)
STEP 2 : Decide the level of significance and draw the graph showing the critical value
The level of significance has been set by the problem at the 5% level. Because this is two-tailed test one-half of the alpha value will be in the upper tail and one-half in the lower tail as shown on the graph. The critical value for the normal distribution at the 95% level of confidence is 1.96. This can easily be found on the student’s t-table at the very bottom at infinite degrees of freedom remembering that at infinity the t-distribution is the normal distribution. Of course the value can also be found on the normal table but you have go looking for one-half of 95 (0.475) inside the body of the table and then read out to the sides and top for the number of standard deviations.
STEP 3 : Calculate the sample parameters and critical value of the test statistic.
The test statistic is a normal distribution, Z, for testing proportions and is:
For this case, the sample of 100 found 53 of these loans were smaller than those of other borrowers. The sample proportion, p′ = 53/100= 0.53 The test question, therefore, is : “Is 0.53 significantly different from .50?” Putting these values into the formula for the test statistic we find that 0.53 is only 0.60 standard deviations away from .50. This is barely off of the mean of the standard normal distribution of zero. There is virtually no difference from the sample proportion and the hypothesized proportion in terms of standard deviations.
STEP 4 : Compare the test statistic and the critical value.
The calculated value is well within the critical values of ± 1.96 standard deviations and thus we cannot reject the null hypothesis. To reject the null hypothesis we need significant evident of difference between the hypothesized value and the sample value. In this case the sample value is very nearly the same as the hypothesized value measured in terms of standard deviations.
STEP 5 : Reach a conclusion
The formal conclusion would be “At a 5% level of significance we cannot reject the null hypothesis that 50% of first-time borrowers take out smaller loans than other borrowers.” Notice the length to which the conclusion goes to include all of the conditions that are attached to the conclusion. Statisticians, for all the criticism they receive, are careful to be very specific even when this seems trivial. Statisticians cannot say more than they know, and the data constrain the conclusion to be within the metes and bounds of the data.
Try It 9.11
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. The teacher performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.
Example 9.12
Suppose a consumer group suspects that the proportion of households that have three or more cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three or more cell phones.
Here is an abbreviate version of the system to solve hypothesis tests applied to a test on a proportions.
Try It 9.12
Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.
Example 9.13
The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.
1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98; 1.02; .95; .95 Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05.
Let’s follow a four-step process to answer this statistical question.
- H 0 : μ ≤ 1
- H a : μ > 1
- Plan : We are testing a sample mean without a known population standard deviation with less than 30 observations. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
- Do the calculations and draw the graph .
- State the Conclusions : We cannot accept the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.
Try It 9.13
The boiling point of a specific liquid is measured for 15 samples, and the boiling points are obtained as follows:
205; 206; 206; 202; 199; 194; 197; 198; 198; 201; 201; 202; 207; 211; 205
Is there convincing evidence that the average boiling point is greater than 200? Use a significance level of 0.1. Assume the population is normal.
Example 9.14
In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.
- H 0 : p ≤ 0.00034
- H a : p > 0.00034
If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.
- We will be testing a sample proportion with x = 172 and n = 420,019. The sample is sufficiently large because we have np' = 420,019(0.00034) = 142.8, nq' = 420,019(0.99966) = 419,876.2, two independent outcomes, and a fixed probability of success p' = 0.00034. Thus we will be able to generalize our results to the population.
Try It 9.14
In a study of 390,000 moisturizer users, 138 of the subjects developed skin diseases. Test the claim that moisturizer users developed skin diseases at a greater rate than that for non-moisturizer users (the rate of skin diseases for non-moisturizer users is 0.041%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/introductory-business-statistics-2e/pages/1-introduction
- Authors: Alexander Holmes, Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Introductory Business Statistics 2e
- Publication date: Dec 13, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/introductory-business-statistics-2e/pages/1-introduction
- Section URL: https://openstax.org/books/introductory-business-statistics-2e/pages/9-4-full-hypothesis-test-examples
© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Data Science Duniya
Learn Data Science, Machine Learning and Artificial Intelligence

Practice Problems on Hypothesis Testing
In this post I have put together the practice problems (from my academics study notes) to explain how in practical Hypothesis Testing works. This post is written mostly for the learners who want to deep dive into the statistics for data science. Focus will be on problem solving. For concepts please refer my previous posts on testing of hypothesis.
Prerequisite to understand Hypothesis testing examples:
- Understanding of hypothesis testing concepts
- How to use z-table, t-table and chi square table.
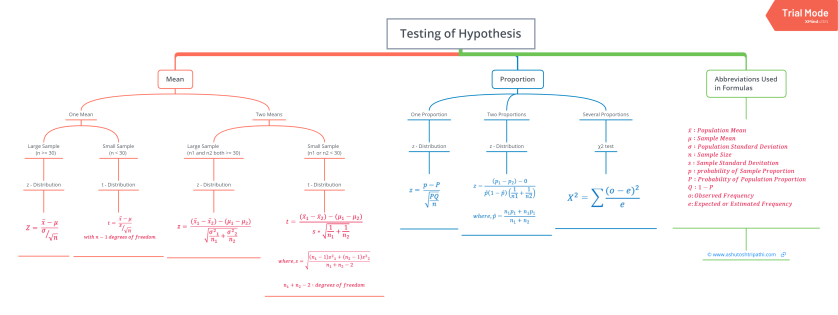
Formula list:
Critical Regions
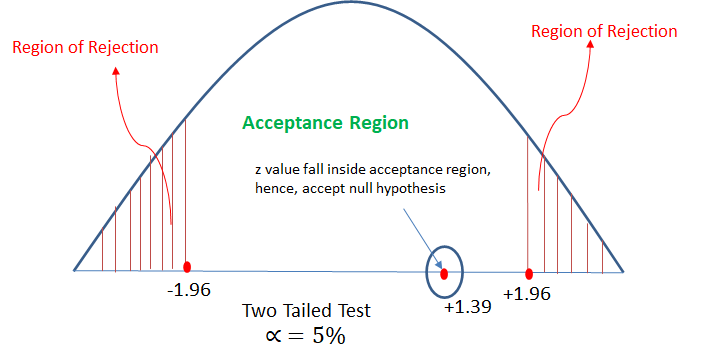
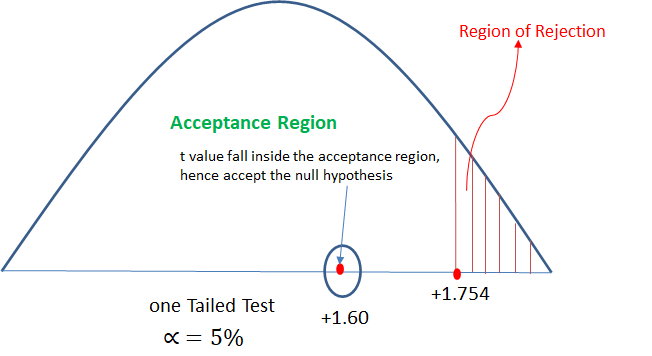
In hypothesis testing, critical region is represented by set of values, where null hypothesis is rejected. So it is also know as region of rejection. It takes different boundary values for different level of significance. Below info graphics shows the region of rejection that is critical region and region of acceptance with respect to the level of significance 1%.

| LoS -> | α = 1% | α = 5% | α = 10% |
|---|---|---|---|
| Two Tailed Test | (-2.58, +2.58) | (-1.96, +1.96) | (-0.645, +0.645) |
| Right Tailed Test | +2.33 | +1.645 | +1.28 |
| Left Tailed Test | -2.33 | -1.645 | -1.28 |
A Telecom service provider claims that individual customers pay on an average 400 rs. per month with standard deviation of 25 rs. A random sample of 50 customers bills during a given month is taken with a mean of 250 and standard deviation of 15. What to say with respect to the claim made by the service provider?
From the data available, it is observed that 400 out of 850 customers purchased the groceries online. Can we say that most of the customers are moving towards online shopping even for groceries?

It is found that 250 errors in the randomly selected 1000 lines of code from Team A and 300 errors in 800 lines of code from Team B. Can we assume that team B’s performance is superior to that of A.
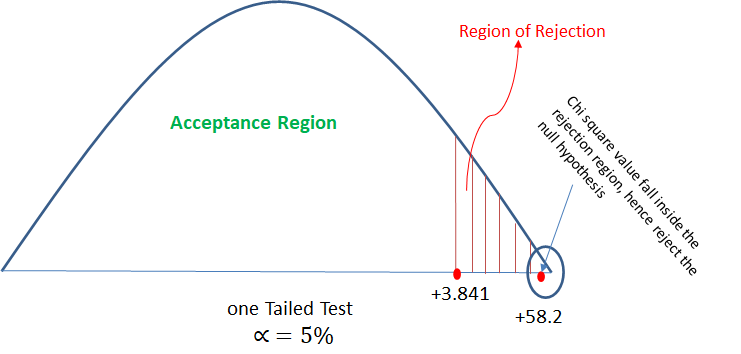
Following is the record of number of accidents took place during the various days of the week.
| Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|
| 120 | 140 | 200 | 90 | 140 | 120 | 180 |
Can we conclude that accident s are independent of the day of week?
| Observed (o) | Expected (e = average of Observed values) | χ2 = [(o-e) ]/e |
|---|---|---|
| 120 | 110 | 0.909 |
| 140 | 110 | 8.181 |
| 200 | 110 | 73.636 |
| 90 | 110 | 3.636 |
| 140 | 110 | 8.181 |
| 120 | 110 | 0.909 |
| 180 | 110 | 44.545 |
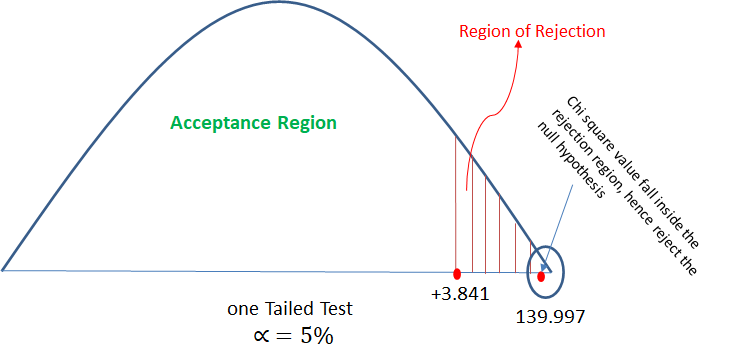
Analyze the below data and tell whether you can conclude that smoking causes cancer or not?
| Category | Diagnosed as Cancer | Without Cancer | Total |
|---|---|---|---|
| Smokers | 400 | 300 | 700 |
| Non-Smokers | 300 | 500 | 800 |
| Total | 700 | 800 | 1500 |
| Category | Diagnosed as Cancer | Without Cancer | Total |
|---|---|---|---|
| Smokers | o = 400, e = 700*700/1500 = 326 | o = 300, e = 700*800/1500 = 373 | 700 |
| Non-Smokers | o = 300, e = 800*700/1500 = 373 | o = 500, e = 800*800/1500 = 426 | 800 |
| Total | 700 | 800 | 1500 |
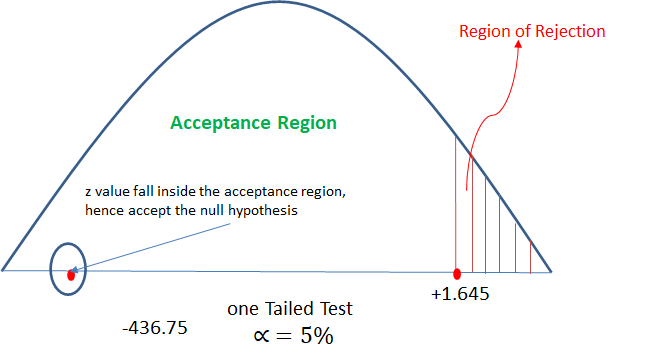
It is claimed that the mean of the population is 67 at 5% level of significance. Mean obtained from a random sample of size 100 is 64 with SD 3. Validate the claim.
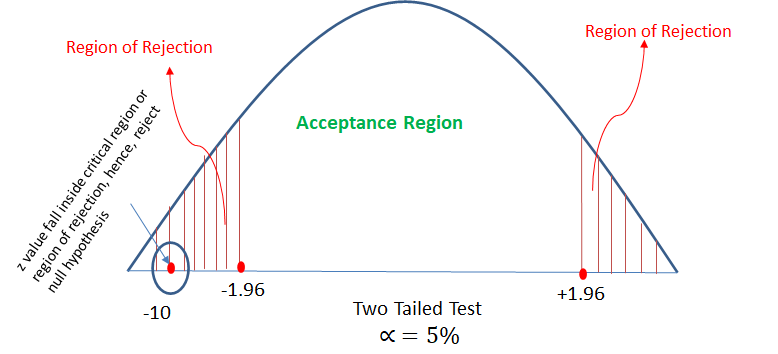
There is an assumption that there is no significant difference between boys and girls with respect to intelligence. Tests are conducted on two groups and the following are the observations
| Mean | Standard Deviation | Size | |
|---|---|---|---|
| Girls | 75 | 8 | 60 |
| Boys | 73 | 10 | 100 |
Validate the claim with 5% LoS (Level of Significance)
An automobile tyre manufacturer claims that the average life of a particular grade of tyre is more than 20,000 km. A random sample of 16 tyres is having mean 22,000 km with a standard deviation of 5000 km.
Validate the claim of the manufacturer at 5% LoS.
That is all for now. Please share your thoughts using the comment section below.
Type your email…
Share this:
- Click to share on Twitter (Opens in new window)
- Click to share on Facebook (Opens in new window)
- Click to print (Opens in new window)
- Click to email a link to a friend (Opens in new window)
- Click to share on LinkedIn (Opens in new window)
- Click to share on Reddit (Opens in new window)
- Click to share on WhatsApp (Opens in new window)
- Click to share on Tumblr (Opens in new window)
- Click to share on Pinterest (Opens in new window)
- Click to share on Pocket (Opens in new window)
- Click to share on Telegram (Opens in new window)
I think smoking problem is wrongly concluded. There the H0 is assumed of dependency(smoking and cancer are dependent) while for chi square test, the null hypothesis is always for independence. So the H0 should be “Smoking and Cancer are independent”.
Please how can I download this page?
In the last sum the alternate hypothesis is less than 22,000 and the null hypothesis is more than 20,000. If the value turns out to be 21,000 then which hypothesis will you accept? I guess there’s an error, the alternate hypothesis should be less than equal to 20,000 and not 22,000. Correct me if I’m wrong.
Thanks for presenting above test cases, it really really helps to understand the tail concept. I am reading z-test and refer your hypothesis page as an example. I go through z-test example and in example no.8 last one it is “One tail – Left tailed test” but in the diag below it shows the right tailed. Not sure am I interpret wrong or diag error ? pls . correct me. Thanks.
The alternate hypothesis is the opposite of null hypothesis so it’s less less than or left tailed. Since the null hypothesis was accepted the graph is Right Tailed had the null hypothesis been rejected or the alternate hypothesis been accepted the graph would have been left tailed. I hope I cleared your doubt
Leave a Reply Cancel reply
This site uses Akismet to reduce spam. Learn how your comment data is processed .

- Already have a WordPress.com account? Log in now.
- Subscribe Subscribed
- Copy shortlink
- Report this content
- View post in Reader
- Manage subscriptions
- Collapse this bar
Hypothesis Testing: Questions and Answers (Biostatistics Notes)
(1). what is hypothesis.
A hypothesis is a statement or an assumption about a phenomenon or a relationship between variables. It is a proposed explanation for a set of observations or an answer to a research question.
In research, hypotheses are tested through experiments or data analysis using a test statistic . The aim of hypothesis testing is to determine if the evidence supports or rejects the hypothesis. If the evidence supports the hypothesis, it provides evidence for the validity of the hypothesis. If the evidence does not support the hypothesis, it may need to be revised or rejected and a new hypothesis may be proposed.
Learn more: Testing of Hypothesis: Theory and Steps
They hypotheses may be directional or non-directional . Directional hypotheses specify the direction of the relationship between the variables , whereas the non-directional hypotheses only state the presence of a relationship without specifying the direction.
(2). What is Hypothesis Testing in Statistics?
It is a method used to make a decision about the validity of the hypothesis concerning a population parameter based on a random sample from that population. It involves the calculation of a test statistic, and the comparison of this test statistic to a critical value determined from the distribution of that test statistic. The decision is made by comparing the p-value (p-value is described below) with a significance level, typically 0.05. If the p-value is less than the significance level, the null hypothesis is rejected and the alternative hypothesis is accepted.
Learn more: Graphical Representation of Data
(3). What is Test-Statistic?
A test statistic is a numerical value calculated from the sample data. It is used to test the hypothesis about a population parameter. Test-statistic summarizes the sample information in to a single value and helps to determine the significance of the results. The choice of test statistic depends on the specific hypothesis test being conducted and the type of data. Commonly used test statistics are t-statistic (t-test), z-statistic (z-test), F-statistic (F-test) and the chi-squared statistic ( Chi-square test ). The test statistic is used in conjunction with a critical value and a p-value to make inferences about the population parameter and determine whether the null hypothesis should be rejected or not.
(4). What is null hypothesis?
The null hypothesis is a statement in statistical testing that assumes no significant difference exists between the tested variables or parameters. It is usually denoted as H0 and serves as a starting point for statistical analysis. The null hypothesis is tested against an alternative hypothesi s, which is the opposite of the null hypothesis and represents the researchers’ research question or prediction of an effect. The aim of statistical testing is to determine whether the evidence in the sample data supports the rejection of the null hypothesis in favor of the alternative hypothesis. If the null hypothesis can’t be rejected, it doesn’t mean it’s proven to be true, it just means that the data do not provide enough evidence to support the alternative hypothesis.
(5). What is alternate hypothesis?
The alternative hypothesis is a statement in statistical testing that contradicts or negates the null hypothesis and represents the researchers’ research hypothesis. Alternate hypothesis is denoted as H1 or Ha . The alternative hypothesis is what the researcher is hoping to prove through the statistical analysis. If the results of the analysis provide strong evidence, the null hypothesis is rejected in favor of the alternative hypothesis. The alternative hypothesis typically represents a non-zero difference or a relationship between variables, whereas the null hypothesis assumes no difference or relationship.

(6). What is Level of Significance in Statistics?
The level of significance in statistics refers to the threshold of probability or p-value below which a result or finding is considered statistically significant. It means that, it is unlikely to have occurred by chance. Level of significance is usually set at 5% (0.05) and indicates the maximum probability of accepting the null hypothesis when it is actually false (Type I error).
Learn more: Difference between Type-I and Type-II Errors
(7). What are statistical errors?
Statistical errors are mistakes can occur during the process of statistical analysis. There are two types of statistical errors: Type I errors and Type II errors.
(8). What is type-I error in statistics?
The type I error, also known as a false positive, is a statistical error that occurs when the null hypothesis is rejected when it is actually true. In other words, a Type I error occurs when a significant result is obtained by chance, leading to the incorrect conclusion that there is a real effect or relationship present.
In hypothesis testing, the level of significance (alpha) is used to control the probability of making a Type I error. A level of significance of 0.05, for example, means that there is a 5% chance of rejecting the null hypothesis when it is actually true. The level of significance is a threshold that is used to determine whether the observed result is significant enough to reject the null hypothesis. Minimizing Type I errors is important in statistical analysis because a false positive can lead to incorrect conclusions and misguided decisions.
(9). How to reduce the chance of committing a type-I error?
There are several ways to reduce the chance of committing a Type I error, they are:
Ø Increasing the sample size: Increasing the sample size increases the precision and power of the statistical test. High sample size reduces the probability of observing a significant result by chance.
Ø Decreasing the level of significance (alpha) : Decreasing the level of significance reduces the probability of rejecting the null hypothesis when it is actually true. A lower level of significance increases the threshold for rejecting the null hypothesis, making it less likely that a Type I error will occur.
Ø Conducting a replication study : Replicating the study with a new sample of data helps to confirm or refute the results and reduces the chance of observing a false positive result by chance.
Ø Using more stringent statistical methods : More sophisticated statistical methods, such as Bayesian analysis, can provide additional information to help reduce the probability of making a Type I error.
Ø Careful interpretation of results : Proper interpretation of results and thorough understanding of the underlying statistical methods used can also help reduce the chance of making a Type I error.
It is very important have a balance in reducing Type I errors with the risk of increasing the chance of making a Type II error. The statistical analysis implemented with an aim of reducing the chance of a Type I error may also the chance of a Type II error.
(10). What is type-II error in statistics?
Type II error, also known as a false negative , is a statistical error that occurs when the null hypothesis is not rejected when it is actually false. In other words, a Type II error occurs when a significant difference or relationship is not detected in the data, despite its existence in the population.
In hypothesis testing, the probability of making a Type II error is represented by beta ( beta error ) and is related to the sample size and the magnitude of the effect being tested. The larger the sample size or the larger the effect, the lower the probability of making a Type II error.
Minimizing Type II errors is important because a false negative can lead to incorrect conclusions and missed opportunities for discovery. To reduce the probability of a Type II error, researchers may use larger sample sizes, increase the level of significance (alpha), or use more powerful statistical methods.
(11). How to reduce the chance of committing the type-II error in statistics?
There are several ways to reduce the chance of committing a Type II error in statistics, they are:
Ø Increasing the sample size : Increasing the sample size increases the precision and power of the statistical test. Increased sample size reduces the probability of failing to detect a significant result.
Ø Increasing the level of significance (alpha): Increasing the level of significance reduces the probability of failing to reject the null hypothesis when it is actually false. A higher level of significance decreases the threshold for rejecting the null hypothesis, making it more likely that a significant result will be detected.
Ø Using a more powerful statistical test : More powerful statistical tests, such as a two-sample t-test or ANOVA, can increase the ability to detect a significant difference or relationship in the data.
Ø Increasing the magnitude of the effect being tested: A larger effect size makes it more likely that a significant result will be detected, reducing the probability of a Type II error.
Ø Conducting a pilot study: A pilot study can provide an estimate of the sample size needed for the main study, increasing the ability to detect a significant result.
It’s important to balance reducing the probability of a Type II error with the risk of increasing the chance of making a Type I error. A statistical analysis that offers to reduce the chance of a Type II error may also increase the chance of a Type I error.
(12). What is p-value?
The p-value is a statistical measure that represents the probability of obtaining a result as extreme or more extreme than the one observed, given that the null hypothesis is true. In other words, the p-value is the probability of observing the data if the null hypothesis is true.
In hypothesis testing, the p-value is compared to the level of significance (alpha) to determine whether the null hypothesis should be rejected in favor of the alternative hypothesis. If the p-value is less than the level of significance, the null hypothesis is rejected, and the result is considered statistically significant. A small p-value indicates that it is unlikely that the result was obtained by chance, and provides evidence against the null hypothesis.
It’s important to note that the p-value does not indicate the magnitude of the effect or the likelihood of the alternative hypothesis being true. It only provides information about the strength of the evidence against the null hypothesis. A low p-value is not proof of the alternative hypothesis, but it does provide evidence against the null hypothesis and supports the conclusion that the effect or relationship is real.
(13). What is the importance of hypothesis testing in research?
Hypothesis testing is an important tool in research as it allows researchers to test their ideas and make inferences about a population based on a sample of data. It provides a systematic and objective approach for evaluating the evidence and making decisions about the validity of a claim.
Evaluating claims : Hypothesis testing provides a way to evaluate claims and determine if they are supported by the data. By testing hypotheses and comparing the results to a predetermined level of significance, researchers can determine if their ideas are supported by the data.
Making decisions : Hypothesis testing helps researchers make decisions about the validity of their ideas and the direction of their research. It provides a way to determine if a claim is supported by the data.
Enhancing the quality of research : Hypothesis testing ensures that research is conducted in a systematic and rigorous manner, which enhances the quality and validity of the research findings. By using a hypothesis testing framework, researchers can ensure that their results are not due to chance and that their conclusions are based on valid evidence.
Understanding the phenomena : By testing hypotheses and evaluating the evidence, hypothesis testing helps researchers gain a better understanding of the phenomena they are studying. It provides a way to determine if a claim is supported by the data and to gain insights into the underlying relationships and patterns in the data.
(14). What are the different types of hypothesis testing tools (test-statistics) available in statistics?
There are several different types of hypothesis testing tools available in statistics which are summarized below. The choice of which tool to use depends on the research question, the type of data being analyzed, and the underlying assumptions of the test.
Z-test: A Z-test is used to test the mean of a population when the population standard deviation is known. It is commonly used to test the difference between two means.
t-test: A t-test is used to test the mean of a population when the population standard deviation is unknown. It is commonly used to test the difference between two means. t-test is performed when the sample size is small (n<30).
ANOVA : Analysis of Variance (ANOVA) is a hypothesis testing tool used to test the equality of means for two or more groups. It is used to determine if there are significant differences among the means of multiple groups. Here comparison between and within groups are done to find out the significance.
Chi-Square Test : The Chi-Square Test the discrepancies between the observed and expected data. It is used to test the independence of two categorical variables. It is commonly used to test if there is a relationship between two categorical variables.
F-test: F-test is variance ratio test. An F-test is used to test the equality of variances for two or more groups. It is commonly used in ANOVA to determine if the variances of the groups are equal.
Non-Parametric Tests : Non-parametric tests are hypothesis tests that do not assume a normal distribution of the data. Examples include the Wilcoxon rank-sum test, the Kruskal-Wallis test, and the Mann-Whitney U test.
(15). What is statistical power?
Statistical power is the probability of correctly rejecting a false null hypothesis in a statistical hypothesis test. It is the complement of the probability of making a type II error, which is failing to reject a false null hypothesis.
The power of a hypothesis test is determined by several factors such as sample size, the effect size, the level of significance and the variability of the data. Increasing the sample size, reducing the variability of the data, or increasing the effect size will generally increase the power of the test.
The power of a hypothesis test is an important consideration in the design of experiments and the selection of sample sizes, as it affects the ability of the test to detect meaningful differences between groups or to reject false null hypotheses. It is also important to consider the trade-off between the power of the test and the level of significance, as increasing the power of the test typically requires a decrease in the level of significance.
Learn more: Principles of Experimental Designs
Learn More : Different Types of Experimental Designs
(16). What is one-tailed and two-tailed test in statistics?
A one-tailed test and a two-tailed test are two types of statistical hypothesis tests used to determine if there is a significant difference between two groups or if a relationship exists between two variables.
A one-tailed test is a hypothesis test that tests the direction of the relationship between two variables. For example, if a researcher wants to determine if a new drug is better than a placebo, a one-tailed test would be used. In a one-tailed test, the alternative hypothesis specifies the direction of the difference, either the new drug is better than the placebo or it is not.
A two-tailed test , on the other hand, does not specify the direction of the difference between the two groups or variables. It only tests if there is a significant difference between the two groups or variables in either direction. For example, if a researcher wants to determine if a new drug is different from a placebo, a two-tailed test would be used. In a two-tailed test, the alternative hypothesis states that the new drug is different from the placebo but does not specify in which direction the difference lies (example- the efficiency may be less or more).
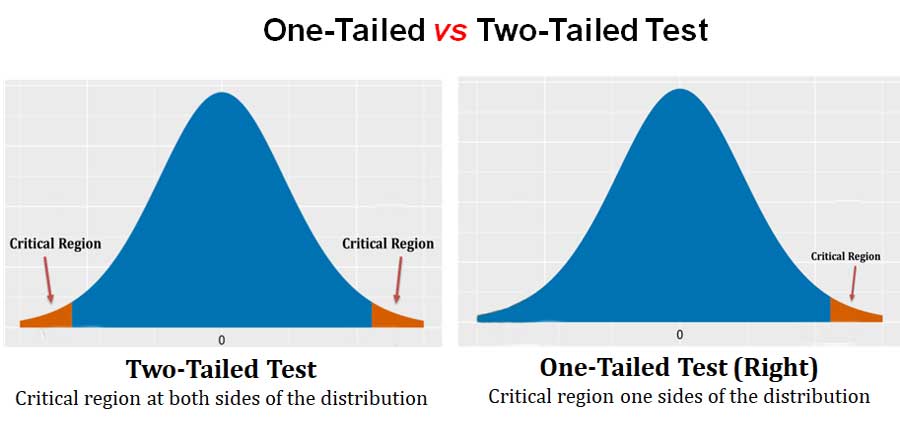
The choice between a one-tailed and a two-tailed test depends on the research question, the data, and the underlying assumptions of the test. One-tailed tests are typically used when the direction of the difference is already known or when the research question is very specific, while two-tailed tests are used when the direction of the difference is not known or when the research question is more general.
(17). What is critical region?
In statistical hypothesis testing, a critical region is the set of values of a test statistic for which the null hypothesis is rejected. The critical region is determined by the level of significance, which is the probability of making a type I error, or incorrectly rejecting a true null hypothesis.
The critical region is often defined as the region of the distribution of the test statistic that is beyond a certain threshold. The threshold is determined by the level of significance and the type of test being conducted (one-tailed or two-tailed). If the calculated test statistic falls within the critical region, the null hypothesis is rejected and the alternative hypothesis is accepted. If the calculated test statistic falls outside of the critical region, the null hypothesis is not rejected. Thus, the critical region is a key component of hypothesis testing, as it determines the decision rule for accepting or rejecting the null hypothesis.
<<< Back to Biostatistics Notes Page
Dear readers
I hope you have enjoyed reading this article and finding the content informative. We believe that this article helped you to understand the Hypothesis Testing Questions and Answers . I would like to take this opportunity to request your COMMENTS on the topics I have covered. Whether you have a suggestion, a question about the topic, or simply want to share your thoughts, I would love to hear from you. Your comments provide me with the opportunity to engage in meaningful discussion and continue to write with the best possible content in Biology.
So, please don’t hesitate to leave a comment below. I appreciate your support and look forward to hearing from you. Best regards, [Admin, EasyBiologyClass]
Related posts:
- Hypothesis Testing in Statistics – Short Notes + PPT
- Graphical Representation of Data (Frequency Polygon, Frequency Curve, Ogive and Pie Diagram)
- What is Data in Statistics?
- Principles of Experimental Designs in Statistics – Replication, Randomization & Local Control
- Types of Experimental Designs in Statistics (RBD, CRD, LSD, Factorial Designs)
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Privacy Overview
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |

Best hypothesis testing questions and answers

Home » Questions » Best hypothesis testing questions and answers
Hypothesis testing is a fundamental concept in statistics that allows us to make informed decisions based on data analysis. It involves formulating a hypothesis about a population parameter and then using sample data to either accept or reject the hypothesis. However, understanding the intricacies of hypothesis testing can be challenging for many individuals. In this article, we will provide a comprehensive list of hypothesis testing questions and answers to help you grasp this concept better.
Before diving into the questions and answers, it is essential to have a basic understanding of hypothesis testing. The process typically involves the following steps:
- Formulating the null and alternative hypotheses.
- Collecting and analyzing sample data.
- Determining the appropriate statistical test based on the data and hypothesis.
- Calculating the test statistic and p-value.
- Comparing the p-value with the significance level to make a decision.
See these Hypothesis Testing Questions and Answers
- What is hypothesis testing?
- What is a null hypothesis?
- What is an alternative hypothesis?
- What is a Type I error?
- What is a Type II error?
- What is a p-value?
- How do you determine the significance level?
- What is a one-tailed test?
- What is a two-tailed test?
- What is the critical region?
- What is the test statistic?
- What is the difference between a sample and a population?
- What is a random sample?
- What is the Central Limit Theorem?
- What is the formula for a z-test?
- What is the formula for a t-test?
- What is the formula for a chi-square test?
- What is the formula for an F-test?
- What is the formula for the test statistic?
- What is the formula for the p-value?
- What is the critical value?
- What is the difference between a one-sample and two-sample test?
- What is a paired t-test?
- What is an independent t-test?
- What is a chi-square goodness-of-fit test?
- What is a chi-square test of independence?
- What is a chi-square test of homogeneity?
- What is an ANOVA test?
- What is the difference between a one-way and two-way ANOVA?
- What is a post hoc test?
- What is a Bonferroni correction?
- What is a power analysis?
- What is effect size?
- What is a confidence interval?
- What is the difference between a null and non-null hypothesis?
- What is statistical significance?
- What is practical significance?
- What is a critical region?
- What is a rejection region?
- What is the difference between a one-tailed and two-tailed test?
- What is a paired sample?
- What is an independent sample?
- What is a population parameter?
- What is a sample statistic?
This list of hypothesis testing questions and answers provides a starting point for your understanding of this statistical concept. By familiarizing yourself with these questions, you will be better equipped to navigate hypothesis testing and make informed decisions based on data analysis.
Related Post:

Leave a Comment Cancel reply
Save my name, email, and website in this browser for the next time I comment.

Best work valentines quotes

Best work quotes for tuesday

Best work ethic quotes

Best work engagement quotes

Best work colleague quotes

Best work bullshit quotes

© the narratologist 2024
Full-Length SAT Suite Practice Tests
Find full-length practice tests on Bluebook™ as well as downloadable paper (nonadaptive) practice tests to help you prepare for the SAT, PSAT/NMSQT, PSAT 10, and PSAT 8/9.

COMMENTS
Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are: H0: x¯ = 4.5,Ha: x¯ > 4.5 H 0: x ¯ = 4.5, H a: x ¯ > 4.5.
View Solution to Question 1. Question 2. A professor wants to know if her introductory statistics class has a good grasp of basic math. Six students are chosen at random from the class and given a math proficiency test. The professor wants the class to be able to score above 70 on the test. The six students get the following scores:62, 92, 75 ...
Carry out an appropriate statistical test and interpret your findings. ANSWER . Yes, a paired t-test suggests that the average difference in hours slept (Dalmane - Halcion) = 0.32 is statistically significant (one sided p-value = .018). SOLUTION . This question is asking for a hypothesis test of the equality of two means in the setting of ...
one-tail test, test statistic is z, α = 0 . 05 , critical value ±1.645. • P-value. the probability of obtaining a value of the test statistic that is at least as extreme as the one calculated using sample data given that the null hypothesis is true. calculation of an exact P-value depends on the alternative hypothesis.
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t* were less than -1.6939 (determined using statistical software or a t-table):s-3-3. Since the biologist's test statistic, t* = -4.60, is less than -1.6939, the biologist rejects the null hypothesis.
Unit 12: Significance tests (hypothesis testing) Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values ...
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. The teacher performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.
First, determine what type of test this is, set up the hypothesis test, find the p-value p -value, sketch the graph, and state your conclusion. Answer. Since the problem is about percentages, this is a test of single population proportions. H0: p = 0.85 H 0: p = 0.85. Ha: p ≠ 0.85 H a: p ≠ 0.85. p = 0.7554 p = 0.7554.
χ2 calculation example | χ2 test in hypothesis testing. Step 2: use χ2 table for α = 5% and get χ2 value from the table. from table we got χ2 (critical value at α = 5%) = 3.841 Step 3: compare both χ2 values. The chi-square value of 18.99 is much larger than the critical value of 3.84, so the null hypothesis can be rejected.
Study with Quizlet and memorize flashcards containing terms like A method for testing a claim or hypothesis about a parameter in a population, using data measured in a sample, is called: A) the central limit theorem B) hypothesis testing C) significance testing D) both b and c, The _____ hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be ...
It tests the null hypothesis that the population variances are equal (called homogeneity of variance or homoscedasticity). Suppose the resulting p-value of Levene's test is less than the significance level (typically 0.05).In that case, the obtained differences in sample variances are unlikely to have occurred based on random sampling from a population with equal variances.
When asked to design a complete hypothesis test, follow the 7-step framework below to guide your answer. Articulate each step to share your thought process with the interviewer. Step 1: Formulate the hypotheses. Specify both the null hypothesis and alternative hypothesis. Step 2: Select the statistical test.
Case1: Population is normally or approximately normally distributed with known or unknown variance (sample size n may be small or large), Case 2: Population is not normal with known or unknown variance (n is large i.e. n≥30). 3.Hypothesis: we have three cases. Case I : H0: μ=μ0 HA: μ μ0. e.g. we want to test that the population mean is ...
short answer: Critical values are generally chosen or looked up in a table (based on a chosen alpha). In this video there was no critical value set for this experiment. In the last seconds of the video, Sal briefly mentions a p-value of 5% (0.05), which would have a critical of value of z = (+/-) 1.96.
A random sample of the scores, x, of 100 club members was taken and is summansed by Ex = 8350 where x denotes the sample mean. Test, at the 5% level of significance, changed. and — 15321 the group's belief that the mean score of 85.9 has (8 marks) 6 The lifetime, X hours, of Ever-white camera batteries is normally distributed. The
This statistics video tutorial provides practice problems on hypothesis testing. It explains how to tell if you should Reject the Null Hypothesis or Fail to...
17 Multiple choice questions. Term. A method for testing a claim or hypothesis about a parameter in a population, using data measured in a sample, is called: A) the central limit theorem. B) hypothesis testing. C) significance testing.
A hypothesis is a statement or an assumption about a phenomenon or a relationship between variables. It is a proposed explanation for a set of observations or an answer to a research question. In research, hypotheses are tested through experiments or data analysis using a test statistic. The aim of hypothesis testing is to determine if the ...
1)View SolutionParts (a) and (b): Part (c) - Method 1: […]
I don't manage to see the link between rejecting the hypothesis and the low probability of the observed results. Using the Alien problem. A) 20% of the observed sample is rebellious B) The hypothesis is that 10% are rebellious Let´s simulate to see how likely is (A) to happen.
What is a sample statistic? This list of hypothesis testing questions and answers provides a starting point for your understanding of this statistical concept. By familiarizing yourself with these questions, you will be better equipped to navigate hypothesis testing and make informed decisions based on data analysis.
How to Use the Student Question Bank; Practice Resources for Educators; For K-12 Educators. About the SAT Suite; ... Full-Length SAT Suite Practice Tests Find full-length practice tests on Bluebook™ as well as downloadable paper (nonadaptive) practice tests to help you prepare for the SAT, PSAT/NMSQT, PSAT 10, and PSAT 8/9. ...